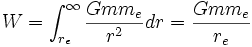Gravitational potential
The above equation leads to the equation for the work done in moving a mass from a radius R to infinity, which is obtained by integrating the force of gravity over this distance:
The work done when moving a mass from infinity to a radius R is therefore
 and this is known as the gravitational potential energy.
and this is known as the gravitational potential energy.
Using the Earth as an example, the work done in moving a mass from the Earth’s surface to infinity is given by:
where G is the universal gravitational constant, m is the object’s mass, re is the Earth’s radius, and me is the Earth’s mass.
General relativity
Newton’s conception and quantification of gravitation held until the beginning of the 20th century, when the German-born physicist Albert Einstein proposed the general theory of relativity. In this theory Einstein proposed that inertial motion occurs when objects are in free-fall instead of when they are at rest with respect to a massive object such as the Earth (as is the case in classical mechanics). The problem is that in flat spacetimes such as those of classical mechanics and special relativity, there is no way that inertial observers can accelerate with respect to each other, as free-falling bodies can do as they each are accelerated towards the center of a massive object.
To deal with this difficulty, Einstein proposed that spacetime is curved by the presence of matter, and that free-falling objects are following the geodesics of the spacetime. More specifically, Einstein discovered the field equations of general relativity, which relate the presence of matter and the curvature of spacetime. The Einstein field equations are a set of 10 simultaneous, non-linear, differential equations whose solutions give the components of the metric tensor of spacetime. This metric tensor allows to calculate not only angles and distances between space-time intervals (segments) measured with the coordinates against which the spacetime manifold is being mapped but also the affine-connection from which the curvature is obtained, thereby describing the spacetime’s geometrical structure. Notable solutions of the Einstein field equations include:
- The Schwarzschild solution, which describes spacetime surrounding a spherically symmetric non-rotating uncharged massive object. For compact enough objects, this solution generated a black hole with a central singularity.
- The Reissner-Nordstr.¶m solution, in which the central object has an electrical charge. For charges with a geometrized length which are less than the geometrized length of the mass of the object, this solution produces black holes with two event horizons.
- The Kerr solution solution for rotating massive objects. This solution also produces black holes with multiple event horizons.
- The cosmological Robertson-Walker solution, which predicts the expansion of the universe.
General relativity has enjoyed much success because of how its predictions have been regularly confirmed. For example:
- General relativity accounts for the anomalous precession of the planet Mercury.
- The prediction that time runs slower at lower potentials has been confirmed by the Pound-Rebka experiment, the Hafele-Keating experiment, and the GPS.
- The prediction of the deflection of light was first confirmed by Arthur Eddington in 1919, and has more recently been strongly confirmed through the use of a quasar which passes behind the Sun as seen from the Earth. See also gravitational lensing.
- The time delay of light passing close to a massive object was first identified by Shapiro in 1964 in interplanetary spacecraft signals.
- Gravitational radiation has been indirectly confirmed through studies of binary pulsars.
- The expansion of the universe (predicted by the Robertson-Walker metric) was confirmed by Edwin Hubble in 1929.
Specifics
Earth’s gravity
Every planetary body, including the Earth, is surrounded by its own gravitational field, which exerts an attractive force on any object that comes under its influence. This field is proportional to the body’s mass and varies inversely with the square of distance from the body. The gravitational field is numerically equal to the acceleration of objects under its influence, and its value at the Earth’s surface, denoted g, is approximately 9.81 m/s² or 32.2 ft/s². This means that, ignoring air resistance, an object falling freely near the earth’s surface increases in speed by 9.81 m/s (around 22 mph) for each second of its descent. Thus, an object starting from rest will attain a speed of 9.81 m/s after one second, 19.62 m/s after two seconds, and so on. According to Newton’s 3rd Law, the earth itself experiences an equal and opposite force to that acting on the falling object, meaning that the earth also accelerates towards the object. However, because the mass of the earth is huge, the acceleration produced on the earth by this same force is negligible.
Equations for a falling body
Under normal earth-bound conditions, when objects move owing to a constant gravitational force a set of kinematical and dynamical equations describe the resultant trajectories. For example, Newton’s law of gravitation simplifies to F = mg, where m is the mass of the body. This assumption is reasonable for objects falling to earth over the relatively short vertical distances of our everyday experience, but is very much untrue over larger distances, such as spacecraft trajectories, because the acceleration far from the surface of the Earth will not in general be g. A further example is the expression that we use for the calculation of potential energy of a body = mgh. This expression can be used only over small distances from the earth. Similarly the expression for the maximum height reached by a vertically projected body,”h = u^2/2g ” is useful for small heights and small initial velocities only. In case of large initial velocities we have to use the principle of conservation of energy to find the maximum height reached.
Gravity and astronomy
The discovery and application of Newton’s law of gravity accounts for the detailed information we have about the planets in our solar system, the mass of the sun, the distance to stars and even the theory of dark matter. Although we haven’t traveled to all the planets nor to the sun, we know their mass. The mass is obtained by applying the laws of gravity to the measured characteristics of the orbit. In space an object maintains its orbit because of the force of gravity acting upon it. Planets orbit stars, stars orbit galactic centers, galaxies orbit a center of mass in clusters, and clusters orbit in superclusters.
Gravity versus gravitation
It is important to note, in some contexts, that gravitation is not gravity, per se. Gravitation is a phenomenon independent of any particular cause. Some theorize that it is possible for gravitation to exist without a force; according to general relativity, that is indeed the case. In common usage “gravity” and “gravitation” are either used interchangeably, or the distinction is sometimes made that “gravity” is specifically the attractive force of the earth, while “gravitation” is the general property of mutual attraction between bodies of matter. In technical usage, “gravitation” is the tendency of bodies to accelerate towards one another, and “gravity” is the force that some theories use to explain this acceleration.
Gravity was rather poorly understood until Isaac Newton formulated his law of gravitation in the 17th century. Newton’s theory is still widely used for many practical purposes, though for more advanced work it has been supplanted by Einstein‘s general relativity. While a great deal is now known about the properties of gravity, the ultimate cause of gravitation remains an open question and gravity remains an important topic of scientific research.
Applications
A vast number of mechanical contrivances depend in some way on gravity for their operation. For example, a height difference can provide a useful pressure differential in a liquid, as in the case of an intravenous drip or a water tower. The gravitational potential energy of water can be used to generate hydroelectricity as well as to haul a tramcar up an incline, using a system of water tanks and pulleys; the Lynton and Lynmouth Cliff Railway [1] in Devon, England employs just such a system. Also, a weight hanging from a cable over a pulley provides a constant tension in the cable, including the part on the other side of the pulley to the weight.
Examples are numerous: For example molten lead, when poured into the top of a shot tower, will coalesce into a rain of spherical lead shot, first separating into droplets, forming molten spheres, and finally freezing solid, undergoing many of the same effects as meteoritic tektites, which will cool into spherical, or near-spherical shapes in free-fall. Also, a fractionation tower can be used to manufacture some materials by separating out the material components based on their specific gravity. Weight-driven clocks are powered by gravitational potential energy, and pendulum clocks depend on gravity to regulate time. Artificial satellites are an application of gravitation which was mathematically described in Newton’s Principia.
Gravity is used in geophysical exploration to investigate density contrasts in the subsurface of the Earth. Sensitive gravimeters use a complicated spring and mass system (in most cases) to measure the strength of the “downward” component of the gravitational force at a point. Measuring many stations over an area reveals anomalies measured in mGal or microGal (1 gal is 1 cm/s^2. Average gravitational acceleration is about 981 gal, or 981,000 mGal.). After corrections for the obliqueness of the Earth, elevation, terrain, instrument drift, etc., these anomalies reveal areas of higher or lower density in the crust. This method is used extensively in mineral and petroleum exploration, as well as time-lapse groundwater modeling. The newest instruments are sensitive enough to read the gravitational pull of the operator standing over them.
Alternative theories
Historical alternative theories
- Aristotelian theory of gravity
- Le Sage’s theory of gravitation (1784) also called LeSage gravity, proposed by Georges-Louis Le Sage, based on a fluid-based explanation where a light gas fills the entire universe.
- Nordstr.¶m’s theory of gravitation (1912, 1913), an early competitor of general relativity.
- Whitehead’s theory of gravitation (1922), another early competitor of general relativity.
Recent alternative theories
- Brans-Dicke theory of gravity (1961)
- Induced gravity (1967), a proposal by Andrei Sakharov according to which general relativity might arise from quantum field theories of matter.
- Rosen bi-metric theory of gravity
- In the modified Newtonian dynamics (MOND) (1981), Mordehai Milgrom proposes a modification of Newton’s Second Law of motion for small accelerations.
- The new and highly controversial Process Physics theory attempts to address gravity
- The self-creation cosmology theory of gravity (1982) by G.A. Barber in which the Brans-Dicke theory is modified to allow mass creation.
- Nonsymmetric gravitational theory (NGT) (1994) by John Moffat
- The satirical theory of Intelligent falling (2002, in its first incarnation as “Intelligent grappling”)
- Tensor-vector-scalar gravity (TeVeS) (2004), a relativistic modification of MOND by Jacob Bekenstein
electrogavitics, magnetogravitics, gravity wave harmonics: electrogravitics: (eg. see books published by integrity research institute [2]) basic principle: electrons push, protons pull – using this principle, Nikola Tesla predicted gravitational repulsion in the 1880s, experimented with it in the 1890s, & designed the cigar shaped aircraft in the early 20th century. The Biefeld-Brown effect (1923) demonstrates this & Thomas Townsend Brown later designed asymetric capacitors suchas the disc shaped aircraft with a negatively electrical charged (repulsion) plate on the bottom & the positively charged (attraction) plate on top. gravity wave harmonics (eg. see book: How to Build a Flying Saucer and Other Proposals in Speculative Engineering, T.B. Pawlicki): gravity is a wave like any other – all the planets rest at harmonic intervals in a standing wave from the source of the wave, the sun.
See also
Notes
- Note 1: Proposition 75, Theorem 35: p.956 – I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton’s Principia, by I. Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
- Note 3: Max Born (1924), Einstein’s Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and Earth.)
References
- ^ Clark, John, O.E. (2004). The Essential Dictionary of Science. Barnes & Noble Books. ISBN 0-7607-4616-8.
- Halliday, David, Robert Resnick; Kenneth S. Krane (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Serway, Raymond A., Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed., Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed., W. H. Freeman. ISBN 0-7167-0809-4.
- Jefimenko, Oleg D., “Causality, electromagnetic induction, and gravitation : a different approach to the theory of electromagnetic and gravitational fields“. Star City [West Virginia] : Electret Scientific Co., c1992. ISBN 0-917406-09-5
- Heaviside, Oliver, “A gravitational and electromagnetic analogy“. The Electrician, 1893.

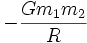 and this is known as the
and this is known as the